💡 'Deep Learning from Scratch'를 참고하여 작성
퍼셉트론(perceptron)은 1957년 프라킁 로젠블라트(Frank Rosenblatt)가 고안한 알고리즘입니다. 딥러닝의 기원이 되는 알고리즘으로 퍼셉트론의 구조를 배우는 것은 딥러닝(deep-learning)을 이해하는데 도움이 됩니다.
1. 퍼셉트론이란?
퍼셉트론은 다수의 신호를 입력 받아 하나의 신호를 출력합니다. 'Deep Learning from Scratch'에서 기술하는 퍼셉트론은 정확히는 '인공 뉴런' 혹은 '단순 퍼셉트론(simple perceptron)'을 의미합니다. 퍼셉트론은 신호를 흐름으로 만들고 정보를 앞으로 전달합니다. 퍼셉트론의 신호는 '신호가 흐른다(1)'와 '신호가 흐르지 않는다(0)' 2가지의 값을 가질 수 있습니다.

그림 1은 퍼셉트론의 예시입니다.
- $ x_1 $과 $ x_2 $는 입력 신호(input), $ y $는 출력 신호(output), $ w_1 $과 $ w_2 $는 가중치(weight)를 의미함
- 그림의 원은 뉴런(neuron) 혹은 노드(node)라 부름
- 입력 신호가 뉴런에 보내질 때, 각각의 고유한 가중치가 곱해짐($ w_1x_1, w_2x_2 $)
- 뉴런에서 보내온 신호의 총합이 임계값($ \theta $)을 넘어설 때만 1을 출력(이를 '뉴런이 활성화한다'라고 표현하기도 함)
이를 수식으로 표현하면 아래와 같습니다.
$$ y = \begin{cases} 0\ (w_1x_1 + w_2x_2 \leq \theta \\ 1\ (w_1x_1 + w_2x_2 > \theta \end{cases} $$
퍼셉트론은 복수의 입력 신호 각각에 고유한 가중치를 부여합니다. 가중치는 각 신호가 결과에 주는 영향력을 조절하는 요소로 작용합니다. 즉, 가중치가 클수록 더 강한 신호를 흘려보내며 이는 해당 신호가 그만큼 더 중요하다는 것을 의미합니다.
2. 단순한 논리 회로
2.1 AND 게이트
AND 게이트는 입력이 둘이고 출력은 하나입니다. 아래의 표 1과 같은 입력 신호와 추력 신호의 대응표를 진리표라고 합니다. 아래의 표는 두 입력이 모두 1일 때만 1을 출력하고, 그 외에는 0을 출력합니다.

2.2 NAND와 OR 게이트
NAND 게이트는 Not AND를 의미하며 AND 게이트를 뒤집은 것입니다. $ x_1 $과 $ x_2 $가 모두 1일 때만 0을 출력하고, 그 외에는 1을 출력합니다. OR 게이트는 입력 신호 가운데 하나 이상이 1이면 출력이 1이 되는 논리회로 입니다.
3. 퍼셉트론 구현
3.1 간단한 구현
1절의 수식을 python으로 구현하면 아래와 같습니다. $ x_1$과 $ x_2 $를 인수로 받는 AND 함수입니다.
def AND(x1: int, x2: int) -> int:
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1 * w1 + x2 * w2
if tmp <= theta:
return 0
else:
return 1매개변수(parameter)인 w1과 w2, theta는 함수 안에서 초기화합니다. 가중치를 곱한 입력의 총합이 임계값을 넘으면 1을 반환하고 그 외에는 0을 반화합니다. 이를 출력하면 아래와 같습니다.
AND(0, 0), AND(1, 0), AND(0, 1), AND(1, 1)
-> (0, 0, 0, 1)3.2 가중치와 편향(Bias) 구현
아래의 식은 $ \theta $를 $ -b $로 치환한 퍼셉트론 식입니다.
$$ y=\begin{cases} 0 (b + w_1x_1 + w_2x_2 \leq 0)\\ 1(b + w_1x_1 + w_2x_2 > 0) \end{cases} $$
여기서 $ b $는 편향을 의미하며 $ w_1 $과 $ w_2 $는 여전히 가중치로 사용합니다. 이 두 개념을 도입한 AND 게이트는 아래와 같이 구현할 수 있습니다.
import numpy as np
def AND(x1: int, x2: int) -> int:
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(x * w) + b
if tmp <= 0:
return 0
else:
return 1여기서 $ -\theta $는 편향 $ b $로 치환되었습니다. 그리고 편향은 가중치 $ w_1, w_2 $와 기능이 다르다는 사실을 알아야 합니다. 가중치 $ w_1 $과 $ w_2 $는 각 입력 신호와 결과에 주는 영향력(중요도)를 조절하는 매개변수입니다. 반면 편향은 뉴런이 얼마나 쉽게 활성화(결과로 1을 출력)되는지 결정하는 매개변수입니다.
NAND와 OR 게이트는 아래와 같이 구현할 수 있습니다.
import numpy as np
def NAND(x1: int, x2: int) -> int:
x = np.array([x1, x2])
w = np.array([-0.5, -0.5]) # AND와 가중치 w, b가 다름
b = 0.7
tmp = np.sum(x * w) + b
if tmp <= 0:
return 0
else:
return 1import numpy as np
def OR(x1: int, x2: int) -> int:
x = np.array([x1, x2])
w = np.array([0.5, 0.5]) # AND와 가중치 b가 다름
b = -0.2
tmp = np.sum(x * w) + b
if tmp <= 0:
return 0
else:
return 14. 퍼셉트론의 한계
4.1 XOR 게이트
XOR 게이트는 배타적 논리합(exclusive or)이라는 논리 회로입니다. 여기서 '배타적'이란, 자기 외에는 거부한다는 의미입니다. 따라서 $ x_1 $과 $ x_2 $ 가운데 한 쪽이 1일 때만 1을 출력합니다.
지금까지 살펴본 퍼셉트론으로는 XOR 게이트를 구현할 수 없습니다. 지금까지의 AND, NAND, OR 게이트는 아래의 그림 2의 왼쪽과 같이 직선 하나로 두 영역을 나눌 수 있었습니다. 하지만 XOR 게이트의 경우, 하나의 직선으로 두 영역을 나누는 것은 불가능합니다.

4.2 선형(Linear)과 비선형(Non-linear)
퍼셉트론은 직선 하나로 나눈 영역만 표현할 수 있다는 한계가 있습니다. 즉, 아래의 그림 3과 같은 곡선은 표현할 수 없습니다. 그림 3과 같은 곡선의 영역을 비선형 영역, 직선의 영역을 선형 영역이라 표현합니다.

5. 다층 퍼셉트론(Multi-layer perceptron)
안타깝게도 단일 퍼셉트론으로는 XOR 게이트를 표현할 수 없었습니다. 하지만 퍼셉트론은 '층(layer)를 쌓아' 다층 퍼셉트론으로 XOR 게이트를 표현할 수 있습니다.
5.1 기존 게이트의 조합
XOR 게이트를 만드는 방법은 다양합니다. 그 중 하나는 앞서 만든 AND와 NAND, OR 게이트를 조합하는 방법입니다. 아래의 그림과 같은 조합이면 XOR 게이트를 구할 수 있습니다.

- $ x_1 $과 $ x_2 $는 입력 신호, $ y $는 출력 신호를 의미
- $ x_1 $과 $ x_2 $는 NAND와 OR 게이트의 입력이 되고, NAND와 OR 게이트의 출력이 AND 게이트의 입력이 됨
- NAND의 출력은 $ s_1 $, OR의 출력은 $ s_2 $라 표현
이를 이용해 진리표를 만들면 아래의 표 2와 같습니다. $ x_1, x_2, y $에 주목하면 XOR의 출력과 같습니다.

5.2 XOR 게이트 구현
지금까지 정의한 함수 AND와 NAND, OR를 이용하면 아래와 같이 쉽게 구현할 수 있습니다.
def XOR(x1: int, x2: int) -> int:
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y이 XOR 함수의 출력은 아래와 같습니다.
XOR(0, 0), XOR(1, 0), XOR(0, 1), XOR(1, 1)
-> (0, 1, 1, 0)XOR은 아래의 그림 4와 같은 다층 구조의 네트워크입니다. 왼쪽부터 차례로 0층, 1층, 2층이라 칭하겠습니다. 그림 4의 퍼셉트론은 모두 3층으로 구성되지만, 파라미터를 갖는 층은 2개에 불과하니 '2층 퍼셉트론'이라 부릅니다. 이렇게 층이 여러 개인 퍼셉트론을 다층 퍼셉트론이라고 합니다. 2층 퍼셉트론의 로직은 다음과 같습니다.
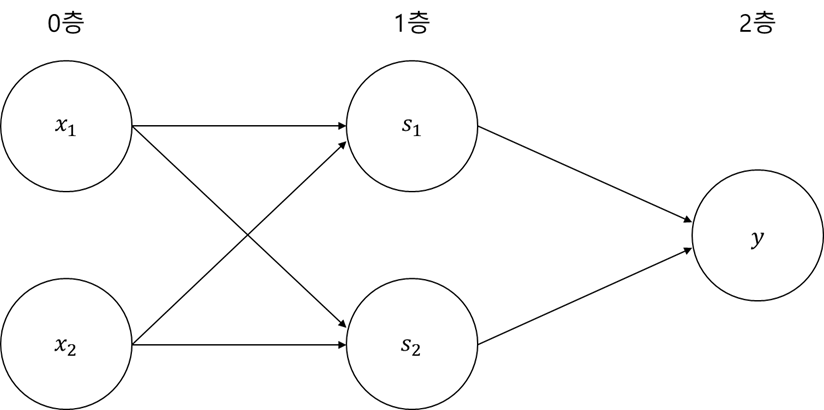
- 0층의 두 뉴런이 입력 신호를 받아 1층의 뉴런으로 신호를 보냄
- 1층의 뉴런이 2층의 뉴런으로 신호를 보내고, 2층의 뉴런은 y를 출력함
이렇게 2층 구조를 활용하여 퍼셉트론으로 XOR 게이트를 구현할 수 있었습니다. 즉, 단층 퍼셉트론으로는 표현할 수 없던 것을 층 하나를 추가함으로써 구현 가능했습니다. 이처럼 퍼셉트론은 층을 쌓아(깊게 하여) 더 다양한 것을 표현할 수 있습니다.
'기초 > 인공지능' 카테고리의 다른 글
| 옵티마이저(Optimizer) (2/2) (0) | 2021.09.02 |
|---|---|
| 옵티마이저(Optimizer) (1/2) (1) | 2021.08.31 |
| 오차역전파(Back-Propagation) (0) | 2021.08.29 |
| 손실 함수(Loss function) (0) | 2021.08.28 |
| 활성화 함수(Activation function) (0) | 2021.08.26 |